Teorie grafuri neorientate
Definitie: Se numeste graf neorientat (G) o pereche ordonata de multimi (X,U), unde X este o multime finita si nevida de elemente, iar U o multime de perechi formate cu elemente distincte din multimea X.
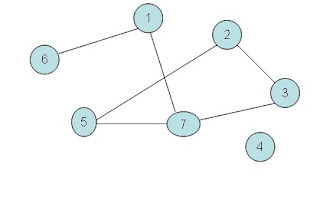
X={1,2,3,4,5,6,7}
U{(1,2),(2,3),(3,7),(7,5),(1,6),(7,1),(2,5),(2,7)}
Terminologie:
- Elementele multimii X se numesc noduri sau varfuri. Multimea X se mai numeste si multimea nodurilor sau varfurilor.
- Ordinul grafului reprezinta numarul de noduri ale grafului.
- Elementele multimii U se numesc muchii. Multimea U se mai numeste si multimea muchiilor.
- Numim noduri adiacente orice pereche de noduri care formeaza o muchie. fiecare din cele doua noduri spunem, ca sunt incidente cu muchia pe care o formeaza.
Exemplu:
Nodul 1 este adiacent cu nodurile 2,6,7; nodul 5 este adiacent cu nodurile 2,7 etc.
Nodurile vecine ale unui nod sunt toate nodurile adiacente cu el.
Se numesc muchii incidente doua muchii care au extremitate comuna.
Exemplu:
Muchiile (1,2) si (2,7) sunt incidente avand ca extremitate comuna nodul 2.(fig.1)
Definitie: Gradul unui nod x al grafului este egal cu numarul muchiilor incidente cu nodul si se noteaza cu d(x).
Exemplu:
d(1)=3;d(2)=4;d(3)=2 etc. (fig.1)
Terminologie:
- Se numeste nod terminal un nod care are gradul egal cu 1.
- Se numeste un nod izolat un nod care are gradul 0.
Exemplu:
Nodul 6 este nod terminal.
Nodul 4 este nod izolat.(fig. 1)
Teoreme:
1. Numarul total de grafuri neorientate cu n noduri este:

2. Suma gradelor tuturor nodurilor unui garf neorientat este egala cu dublul nuamrului de muchii.
3. Daca gaful G neorientat are n noduri, n>2, atunci cel putin 2 noduri au acelasi grad.
4. Pentru orice graf neorientat numarul nodurilor de gard impar este par.
5. Numarul minim de muchii pe care trebuie sa le aiba n graf neorientat cu n noduri , ca sa nu existe noduri izolate este:
Exemplu: {6,1,7,5,2,3} reprezinta un lant.
Exemplu:
{6,1,7,2} reprezinta un lant elementar.
{6,1,7,5,2,7,3} reprezinta lant neelementar.
{2,3,7,5} reprezinta lant simplu.
{5,2,7,5,2,3} reprezinta lant compus.
{5,2,7,5} reprezinta ciclu intr-un lant.(fig.1)
G={X,U}
X={1,2,3,4,5,6,7}
U={(1,6),(1,7),(2,3),(2,5),(3,7),(5,7)}
Definitie: Se numeste subgraf al unui graf notat Gs={Y,U} cu proprietatea ca multimea varfurilor Y este inclusa in multimea varfurilor X si multimea perechiilor de varfuri X este inclusa in multimea perechiilor de varuri U. (Multimea V este formata din valori distincte ale multimii Y)
G={X,U}
X={1,2,3,4,5,6}
U={(1,2),(1,6),(2,3),(2,5)}
Graful null este garful in care multimea U este vida.
Numarul de noduri dintr-un graf complet se poate afla cu formula: n(n-1)/2.
Graful conex este un graf care are intre oricare doua noduri un lant care sa le uneasca.
Teorie cozi
Definitie:
Coada este o lista liniara simplu inlantuita, care se construieste pe "principiul primul intrat, primul iesit".
Coada are doua capete:
Structura de tip FIFO (First-In, First-Out).
Declararea cozii:
struct nod { int x; nod *urm} *p,*u,*q;
q=new nod;
p=q;
u=q;
cin>>q->inf;
q-> urm=NULL;
Citirea cozii:
for(i=1;i<=n;i++)
{
q=new nod;
cin>>q->x;
u->urm=q;
u=q;
u->urm=NULL;
}
Afisarea cozii se face ca si afisarea unei liste simplu inlantuite:
q=p;
while(q!=NULL)
{
cout<<<" ";
q=q->urm;
}
Stergerea:
q=p>urm;
p->urm=p->urm->urm;
delete q;
Adaugarea unui nod:
w=new nod;
w->x=q->x;
q->urm=w;
w=q;
int sub(nod *p, int x)
{
int k=0;
while(p!=NULL)
{
if((p->nr)
p=p->urm;
}
a. p->urm->urm->info=p->info;
2. Într-o listă simplu înlănţuită fiecare element reţine în câmpul urm adresa elementului următor din listă, iar în câmpul inf un număr întreg. Adresa primului element al listei este memorată în variabila prim, variabila p este de acelaşi tip cu prim, iar variabila x este de tip întreg. Iniţial, în listă sunt memorate, în această ordine, numerele de mai jos,. Care este conţinutul listei în urma executării secvenţei de instrucţiuni scrise alăturat?
p=prim;
while(p->urm!=NULL)
{x=p->inf;
p->inf=p->urm->inf;
p->urm->inf=x;
p=p->urm;
}.
a. 2 3 4 5 6 1
b. 6 5 4 3 2 1
c. 2 1 4 3 6 5
d. 1 2 3 4 5 6
Varianta este d) deoarece primul numar este 1 iar urmatoarele elemente (p->urm->inf=2) sunt in ordine consecutiva .
Lanturi intr-un graf neorientat:
Definitie: Se numeste lant intr-un graf neorientat o succesiune de varfuri cu proprietatea ca intre oricare doua varfuri alaturate exista o muchie. Exemplu: {6,1,7,5,2,3} reprezinta un lant.
Terminologie:
- Numim lant elementar o succesune de varfuri care respecta proprietatea de lant si in care oricare doua varfuri sunt distincte. In caz contrar lantul se numeste neelementar.
- Se numeste lant simplu o succesiune de varfuri cu proprietatea ca fiecare muchie este vizitata o singura data.
- Se numeste lant compus un lant in care o muchie este vizitata de cel putin doua ori.
- Se numeste ciclu int-un lant o succesiune de varfuri cu proprietatea ca primul nod coincide cu ultimul nod.
Exemplu:
{6,1,7,2} reprezinta un lant elementar.
{6,1,7,5,2,7,3} reprezinta lant neelementar.
{2,3,7,5} reprezinta lant simplu.
{5,2,7,5,2,3} reprezinta lant compus.
{5,2,7,5} reprezinta ciclu intr-un lant.(fig.1)
Grafuri derivate:
Definitie: Se numeste graf partial notat cu Gp=(X,V), cu proprietatea ca multimea V de perechi de varfuri este inclusa in multimea U.G={X,U}
X={1,2,3,4,5,6,7}
U={(1,6),(1,7),(2,3),(2,5),(3,7),(5,7)}
Definitie: Se numeste subgraf al unui graf notat Gs={Y,U} cu proprietatea ca multimea varfurilor Y este inclusa in multimea varfurilor X si multimea perechiilor de varfuri X este inclusa in multimea perechiilor de varuri U. (Multimea V este formata din valori distincte ale multimii Y)
G={X,U}
X={1,2,3,4,5,6}
U={(1,2),(1,6),(2,3),(2,5)}
Grafuri speciale:
Graful null este garful in care multimea U este vida.
Graful complet cu n noduri este graful care are intre oricare doua noduri adiacente o muchie.
Graful conex este un graf care are intre oricare doua noduri un lant care sa le uneasca.
Teorie cozi
Definitie:
Coada este o lista liniara simplu inlantuita, care se construieste pe "principiul primul intrat, primul iesit".
Coada are doua capete:
- prin capatul din dreapta introducem noduri in coada
- la capatul din stanga extragem noduri din coada.
Structura de tip FIFO (First-In, First-Out).
Declararea cozii:
struct nod { int x; nod *urm} *p,*u,*q;
q=new nod;
p=q;
u=q;
cin>>q->inf;
q-> urm=NULL;
- g->x=informatia utila.
- nod*urm=nodul urmator .
- q=adresa nodului.
Citirea cozii:
for(i=1;i<=n;i++)
{
q=new nod;
cin>>q->x;
u->urm=q;
u=q;
u->urm=NULL;
}
Afisarea cozii se face ca si afisarea unei liste simplu inlantuite:
q=p;
while(q!=NULL)
{
cout<
q=q->urm;
}
Stergerea:
q=p>urm;
p->urm=p->urm->urm;
delete q;
Adaugarea unui nod:
w=new nod;
w->x=q->x;
q->urm=w;
w=q;
int sub(nod *p, int x)
{
int k=0;
while(p!=NULL)
{
if((p->nr)
p=p->urm;
}
Variante bac alocare dinamica
Varianta 36 (Subiectul II)
2. Într-o listă liniară simplu înlănţuită, alocată dinamic, fiecare element reţine în câmpul adr adresa următorului element din listă, iar în câmpul info un număr întreg. Adresa primului element al listei este memorată în variabila p. Ştiind că lista conţine exact 4 elemente, atunci expresia p^.adr^.info reprezintă: (4p.)
a. adresa celui de al doilea element
a. adresa celui de al doilea element
b. adresa celui de al treilea element
c. valoarea memorată în al doilea element
d. valoarea memorată în al treilea element
Raspunsul corect este: c.
Relatia data se scrie de fapt p->urm->adr si retine informatia utila a celui de-al doilea nod din lista.
Varianta 74 (Subiectul II)
1. Într-o listă liniară simplu înlănţuită, cu cel puţin 3 noduri, fiecare element reţine în câmpul urm adresa următorului element din listă, iar în câmpul info informaţia utilă de tip întreg. Dacă variabila p reţine adresa primului element din listă atunci care dintre secvenţele de mai jos atribuie câmpului info al celui de al treilea nod informaţia utilă din primul nod al listei?
a. p->urm->urm->info=p->info;
b. p->urm->urm->info=p->urm->info;
c. p->info->info->info = p->info;
c. p->info->info->info = p->info;
d. p->urm->urm = p->info;
Varianta a ) pune in discutie atribuirea informatiei utile a nodului 3 spre nodul 1 unde p->umr->umr->info ese informatia utila a nodului 3 redirectionata spre nodul 1 - p->info
Varianta 76 (Subiectul II)
p=prim;
while(p->urm!=NULL)
{x=p->inf;
p->inf=p->urm->inf;
p->urm->inf=x;
p=p->urm;
}.
a. 2 3 4 5 6 1
b. 6 5 4 3 2 1
c. 2 1 4 3 6 5
d. 1 2 3 4 5 6
Varianta este d) deoarece primul numar este 1 iar urmatoarele elemente (p->urm->inf=2) sunt in ordine consecutiva .