Variante bac SII V91-95
- grafuri -
Varianta 91 (Subiectul II)
1. Se consideră un graf neorientat G cu 101 noduri şi 101 muchii. Numărul maxim de vârfuri izolate ale grafului poate fi:
a. 0 b. 10 c. 50 d. 86 Raspunsul corect este a.
Conform teoremei, numarul minim de muchii pe care trebuie sa le le aiba un graf neorientat ca sa nu existe noduri izolate este egal cu (n+1)/2,unde n este numarul de noduri.Astfel, avand 101 noduri, dupa aplicarea teoremei rezulta ca trebuie sa existe minim 51 de muchii pentru a nu avea noduri izolate [(101+1)/2=51].
Pentru ca in problema exista 101 muchii numarul de noduri izolate este 0.
2. Un arbore cu 11 noduri, numerotate de la 1 la 11, este memorat cu ajutorul vectorului de taţi t=(2,5,5,3,0,2,4,6,
6,2,3). Descendenţii direcţi (fiii) ai nodului 2 sunt:
a. 1, 6 şi 10 b. 5 c. 6, 8 şi 9 d. 3
Raspunsul corect este a.
Varianta 92 (Subiectul II)
1. Care din următoarele arce aparţine grafului orientat cu 4 varfuri,avand gradele din tabelul alaturat (x,y din N)?
a. (2,3)
b. (1,2)
c. (1,4)
d. (4,1)
Raspunsul corect este b.
Ca verificare am alcatuit matricea de adiacenta si am verificat daca suma gradelor externe ale tuturor varfurilor este egala cu suma gradelor interne si cu numarul muchiilor.
0 1 1 0 Gr int.(1)=0 Gr ext.(1)=2
0 0 0 0 Gr int.(2)=2 Gr ext.(2)=0
0 1 0 1 Gr int.(3)=1 Gr ext.(3)=2
0 0 0 0 Gr int.(4)=1 Gr ext.(4)=0
Suma gradelor externe este egala cu 4.
Suma gradelor interne este egala cu 4.
Numarul muchiilor este egal cu 4.
3. Scrieţi vectorul de ”taţi” corespunzător arborelui cu
8 noduri ,numerotate de la 1 la 8, dat prin lista alăturată a descendenţilor direcţi (fiilor)?
1: 4,6,7 5: -
2: - 6: 2
3: 1,8 7: -
4: - 8: 5
Vectorul de tati este 3 6 0 1 8 1 1 3
Varianta 93 (Subiectul II)
1. Care este numărul minim de noduri ce trebuie eliminate din graful alăturat astfel încât graful parţial obţinut să nu fie conex? a. 3 b. 0
c. 2 d. 1
Raspunsul corect este d.
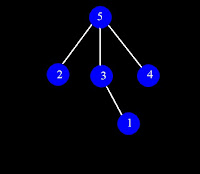
Prin eliminarea nodului 5, graful nu mai este conex.
3. Se consideră arborele din figura alăturată. Care este nodul care trebuie ales ca rădăcină astfel încât vectorul de taţi corespunzător arborelui rezultat să conţină patru elemente egale?
Nodul care trebuie ales ca radacina este 1.
Astfel, vectorul de tati va fi de forma : 0 1 1 1 6 1
Nodurile 2,3,4 si 6 sunt fii ai nodului 1.Varianta 94 (Subiectul II)
1. Care dintre nodurile grafului neorientat cu 5 noduri, numerotate de la 1 la 5, dat prin matricea de adiacenţă alăturată, are gradul cel mai mare?
a. 4 b. 3
c. 5 d. 2
Raspunsul corect este b.
Gradul nodului 3 este egal cu 4.
In cazul in care radacina este varful 5, vectorul de tati corespunzator este: 3 5 5 5 0
2. Un graf cu 5 noduri, numerotate de la 1 la 5, conţine următoarele muchii: [1,2], [1,3],[2,3], [2,5], [3,4], [3,5], [4,5]. Eliminaţi din acest graf numărul necesar de muchii astfel încât graful parţial rezultat să fie arbore. Considerând că acest arbore are ca rădăcină vârful 5, care este vectorul cu legături „de tip tată” corespunzător ?
Indiferent de nodul pe care il alegem ca radacina,trebuie sa eliminam 3 muchii pentru a avea un arbore.
In cazul in care radacina este varful 5, vectorul de tati corespunzator este: 3 5 5 5 0
Varianta 95 (Subiectul II)
1. Câte valori nule pot să apară într-un vector cu legături „de tip tată” asociat unui arbore cu rădăcină care conţine 10 noduri?
a. niciuna b. exact una
c. depinde de configuraţia arborelui d. exact două
Raspunsul corect este b.
Exista o singura valoare nula intr-un vector "de tip tata" deoarece nu poate exista decat o radacina.
3. Scrieţi listele de adiacenţă pentru un graf neorientat, cu 5 noduri, numerotate de la 1 la 5, care are un număr maxim de muchii şi nu este eulerian.
???
4. Se dă graful orientat cu 5 noduri, numerotate de la 1 la 5, definit prin matricea de adiacenţă alăturată. Determinaţi un drum de lungime maximă de la nodul 1 la nodul 5 , care să fie alcătuit din arce distincte două câte două. Scrieţi lungimea drumului determinat precum şi arcele care îl compun (lungimea unui drum este egală cu numărul de arce care îl compun).
Drumul este alcatuit din 5 arce:
(1,2)
(2,4)
(4,3)
(3,2)
(2,5)Variante bac SII V48-50
- liste -
Varianta 48 (Subiectul II)
1. Într-o listă simplu înlănţuită cu cel puţin 3 elemente, fiecare element reţine în câmpul inf un număr natural, iar în câmpul urm adresa elementului următor din listă sau NULL dacă nu există un element următor. Variabila p reţine adresa primului element din listă, iar variabilele q şi aux sunt de acelaşi tip cu p. Dacă se prelucrează lista de mai jos, care va fi conţinutul listei după executarea următoarei secvenţe de instrucţiuni?
q=p;
while(q->urm->urm !=NULL && q->inf >= p->inf)
{q = q->urm;
aux=q->urm;
q->urm=aux->urm;
delete aux;}a.8 5 8 9 3 b. 7 8 8 9 3 c. 7 8 5 8 9 3 d. 7 8 5 9 3
Raspunsul corect este b.
În urma executării programului se elimină al 3-lea nod. (nodul 5)
Varianta 49 (Subiectul II)
4. Într-o listă simplu înlănţuită cu cel puţin 2 elemente, fiecare element reţine în câmpul inf un număr natural, iar în câmpul urm adresa elementului următor din listă sau NULL dacă nu există un element următor. Variabila p reţine adresa primului element din listă, iar variabila q este de acelaşi tip cu p. Dacă se prelucrează lista de mai jos, care va fi conţinutul listei după executarea următoarei secvenţe de instrucţiuni?
q=p;
while(q->urm!=NULL && q->inf<=q->urm->inf)
{q=q->urm;
q->inf=q->urm->inf+1;}Secvenţa se opreşte după prima parcurgere, iar în urma executării ei va rezulta lanţul 1 4 3 5 4 2 . Secvenţa nu a putut fi reluată deoarece în momentul în care informaţia utilă a primit valoarea 4 a devenit mai mare decat informaţia utilă a nodului următor.
Varianta 50 (Subiectul II)
2. Într-o listă simplu înlănţuită cu cel puţin 2 elemente, fiecare element reţine în câmpul inf un număr natural, iar în câmpul urm adresa elementului următor din listă sau NULL dacă nu există un element următor. Variabila p reţine adresa primului element din listă. Dacă se prelucrează lista de mai jos, care este valoarea memorată de variabila întreagă k, la finalul executării următoarei secvenţe de instrucţiuni?
k=3;
while(p->urm!=NULL && p->inf > p->urm->inf)
p = p->urm;
k = k + p->urm->inf;
a. 8 b. 10 c. 12 d. 13
Răspunsul corect este b.
Structura repetitivă se execută până în momentul în care informaţia utilă a unui nod este mai mică decât cea a nodului următor.Atunci lui k i se adaugă valoare informaţiei utile a nodului la care am rămas.
În secvenţă, p continuă sa crească până la nodul 4, a cărui informaţie utilă este 7 (7<10) .Deci, valoarea finală a lui k va fi 10 (3+7).
Teorie stive
Definiţie:
Stiva este o listă liniară simplu înlănţuită care se construieşte pe principiul "ultimul intrat, primul ieşit" (LIFO). Stiva are un singur capăt care se numeşte vârful stivei.
Singurele operaţii admise în stivă sunt adăugarea unui nod în vârful ei şi extragerea unui element tot din vârf.
Crearea stivei:
Înainte de a realiza secvenţa de creare a stivei, acesta trebuie declarată într-o structură:
struct nod { int x;
nod *urm;} *vf,*q;
- unde x ia valoarea informaţiei utile, iar urm adresa elementului următor din listă sau NULL dacă nu există un element următor.
Algoritm pentru creare:
vf=new nod;
vf->urm=NULL;
cin>>vf->x;
În urma aceste secvenţe am creat primul nod şi i-am atribuit o informaţie utilă.
for(i=2;i<=n;i++)
{q=new nod;
q->urm=vf;
vf=q;
cin>>vf->x;}
În continuare am creat si le-am atribuit câte o informaţie utilă următoarelor n noduri.
Afişarea stivei:
while(vf!=NULL)
{cout
vf=vf->urm;}
Afişarea stivei se face începând cu elementul din vârf,cât timp acesta există (este diferit de NULL) după care se trece la vârful următor.
Adăugarea unui element:
q=new nod; // formăm o adresă nouă
cin>>q->x; // citim informaţia utilă
q->urm=vf; // formăm legătura cu vechiul vârf
vf=q; // vârful nou este q
- se face doar în vârful stivei.
q=vf; // q ia valoarea varfului
vf=vf->urm;
delete q; // se sterge varful
